物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第6课。
了解本系列其他文章,请收藏目录:
0) 开篇语
这是本系列的第6课,也是前半部分最重要的一课。
因为本课结束之后,我们就终于要正式踏进量子力学的大门了。
在本系列的前5课中,我们知道,量子力学主要关注的对象,是具有向量性质的抽象的态矢量,那些经典力学量的信息,都以概率形式包含在态矢量之中。
但我们在前面看到的例子,要么是虚构的思想实验(薛定谔的猫 ),要么是几乎只在量子世界里出现的力学量(电子的自旋 ),这都不是我们所熟悉的经典力学量。
那么,我们更为熟悉的经典力学量、比如动量、能量等,又是怎么和态矢量联系起来的呢?
这其实就触碰到量子力学的基本假设了,但讲这个基本假设之前,我们要先回到线性代数中,去找两位老朋友叙叙旧。
1) 特征值与特征向量
我们要见的这两位老朋友,是特征向量和特征值。
也许是出于严谨的考虑,大部分线性代数教材没有告诉我们矩阵、特征向量和特征值有什么几何意义,但这个其实没有什么神秘的,几句话就能说清。
我们先说矩阵本身的几何意义,一个直观理解就是,矩阵通过与向量相乘的形式作用在向量上,对向量进行一种变换“操作”。
比如我们比较熟悉的两个最简单的例子:
一个是旋转矩阵:
$\small \boldsymbol R_{\theta}=\begin{bmatrix} \cos\theta&-\sin\theta\\sin\theta&\cos\theta \end{bmatrix} \quad\scriptsize{(式6.1)}$
它作用在向量上时,会把向量旋转 $\small \theta$ 角而不改变其大小:
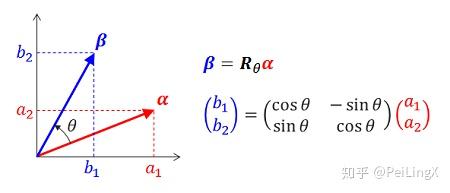
另一个是乘了一个系数的单位矩阵:
$\small {\boldsymbol{\it\Lambda}}=\begin{bmatrix} \lambda&0\\ 0&\lambda \end{bmatrix} \quad\scriptsize{(式6.2)}$
它作用在向量上时,会伸缩一个向量而不改变其方向(这个很明显,就不画图了 )。
但绝大多数矩阵,对向量的“操作”都更复杂,从几何结果来说,不仅同时包括了上面两种,而且在不同的向量上会产生不同的旋转角度和伸缩系数。
不过,对于一些矩阵而言,不管它作用在其他向量上时会造成怎样的改变,我们总是能找到一些特殊的向量,使得这个矩阵只能改变其“大小”,而不改变其方向。
这组向量,就是这个矩阵的特征向量,而它被矩阵作用后“大小”改变的比例,就是相应的特征值。
如果向量 $\small \boldsymbol\alpha$ (假设是列向量 )是矩阵 $\small \boldsymbol A$ 的特征向量,相应的特征值是 $\small \lambda$ ,那么将上面那句话写成数学式,就是我们熟悉的关系:
$\small \boldsymbol A\boldsymbol\alpha=\lambda\boldsymbol\alpha \quad\scriptsize{(式6.3)}$
有了这个认识,我们就能回到量子力学中,理解量子力学最基本的假设,并且将量子态与经典物理量联系起来。
2) 本征值、本征态与测量
我们在第1课提到过,一个经典力学量会对应一组本征态,又叫本征矢(Eigen Vector)。
看到它的英文名,我们一眼就能认出来,它其实就是线性代数中所说的特征向量,只是在量子力学中换了一个中文翻译而已。
既然一组本征态的数学本质就是一组特征向量,那么它背后对应的那个物理量,在量子力学中是不是也会对应一个矩阵呢?
的确是这样,只不过,这个矩阵换成了一个更抽象也更广义的概念,叫作算符(Operator)。
如果某个力学量的符号为 $\small F$ ,那么它的算符就是 $\small F$ 上加个小尖帽,记作 $\small \hat{F}$ (读作F-hat )。
(很多量子力学教材中常常会省略掉小帽子符号,我们还是留着以便区分,不过这只是个习惯问题,不必太纠结 )
有了算符的概念,我们就能将量子态与经典力学量联系起来了。
具体怎么理解呢?
首先,联想到算符是矩阵的推广,我们不难猜到,我们讨论力学量 $\small F$ 的本征态的时候,其实就是在讨论算符 $\small \hat F$ 的本征矢或者叫本征态(就像矩阵的特征向量一样 )。
对于一个矩阵而言,每个特征向量都会有对应的特征值,那么对于算符而言也是如此。
当一个物理对象的量子态正好处于算符 $\small \hat F$ 的某个本征态的时候,我们可以仿照着式6.3写出这样的关系:
$\small \hat{F}\left|F_a\right>=f_a\left|F_a\right> \quad\scriptsize{(式6.4)}$
(其中 $\small \left|F_a\right>$ 是 $\small \hat F$ 的某个本征态 )
而出现在等式右边的 $\small f_a$ 是一个实数,它就代表着本征态 $\small\left|F_a\right>$ 对应的特征值,按照量子力学的习惯翻译,我们将它称为本征值(英文仍然是Eigen Value,只是翻译不同而已 )。
那么现在问题来了:式6.4的“几何意义”是不是也和线性代数中特征值关系式6.3一样,意味着算符 $\small \hat F$ 使态矢量 $\small \left|F_a\right>$ 的“方向”保持不变、“长度”伸缩到了原来的 $\small f_a$ 倍呢?
和线性代数类似的地方是,算符 $\small \hat F$ 的确保持了它的本征态 $\small \left|F_a\right>$ 的“方向”不变的效果,这在量子力学中可以理解为对处于本征态 $\small \left|F_a\right>$ 的物理对象测量力学量 $\small F$ 后,它仍然处于原来的“方向”上。
但是和线性代数不同的地方是“长度”伸缩的问题。
在量子力学中,一个态矢量没有“大小”的概念(我们会在本文最后的附录中解释为什么这么规定 ),对一个态矢量进行“伸缩”后,得到的仍然是同一个态矢量。
也就是说,一个态矢量只取决于它的“方向”,这也就能解释,为什么算符作用在它的本征态上时,这个本征态不会被改变了,因为它的“方向”没变。
但我们知道,线性代数中,矩阵乘以特征向量后会出现一个特征值改变向量的大小,而在量子力学中,既然本征态的“大小”不会变,那么问题来了:这个特征值被藏到哪去了?
这个问题的答案,正好就是联系量子和经典物理的桥梁:
物理量算符作用到本征态上得到的本征值,就是经典世界中测量到的该物理量的值。
比如有一个 $\small x$ 方向上具有确定动量的粒子(这意味着它的量子态正好是动量算符 $\small \hat{p}_x$ 的某个本征态 $\small \left|p_x\right>$ ),去测量它的动量时,测得的动量值 $\small p_x$ ,就是相应的本征值。
对应到数学表达式,就是:
$\small \hat{p}_x\left|p_x\right>=p_x\left|p_x\right> \quad\scriptsize{(式6.5)}$
也就是说,当粒子的量子态处于动量算符的某个本征态 $\small \left|p_x\right>$ 时,我们去测量它的动量后, $\small \left|p_x\right>$ 仍然不会改变,但本征值信息会被“释放”出来,表现成测量仪器上的读数 $\small p_x$
这样,似乎只存在于想象中的不可捉摸的量子幽灵(动量算符 $\small \hat{p}$ 、态矢量 $\small \left|p_x\right>$ )和经典物理中可以“真实”测量到的经典物理量(本例中的动量 $\small p_x$ )就联系起来了。
不过,我们刚刚讨论的只是量子态处于某个力学量本征态的情形,同学们一定会马上问:
假如一个物理对象的量子态不是力学量 $\small F$ 的本征态,而是处于一系列本征态 $\small{\left|F_a\right>} $的叠加态:
$\small \left|\psi\right>=\sum_ac_a\left|F_a\right> \quad\scriptsize{(式6.6)}$
情况又会如何呢?
在前面的课程中,我们已经知道,对于这样的叠加态,我们去测量力学量 $\small F$ 时,它会随机坍缩到 $\small F$ 的本征态当中的一个,相应的概率就是:
$\small P_a=c_a^*c_a=\left|c_a\right|^2 \quad\scriptsize{(式6.7)}$
而对应到本征值上,这就意味着测量仪器会随机测出一个值 $\small f_a$ ,出现这个值的概率为 $\small P_a$
而基于这一点,我们还能计算测量结果的期望值:
$\small \bar{f}=\sum_aP_af_a=\sum_ac_a^*c_af_a \quad\scriptsize{(式6.8)}$
也就是说,对于很多个处于量子态 $\small \left|\psi\right>=\sum_ac_a\left|F_a\right>$ 的物理对象,假如我们去测量力学量 $\small F$ ,那么测量下来的平均结果就是 $\small \bar{f}=\sum_ac_a^*c_af_a$
这个关系有助于我们将来定量计算不确定性关系、也有助于我们将经典动力学与量子态的演化规律联系起来。
具体的我们以后再细说。
接下来,我们来看两个物理上的例子,感受一下算符、本征态和本征值之间的关系。
3) 两个例子
- 第一个例子:SG实验中的自旋磁矩
我们在第4课的SG实验中看到,银原子通过SG实验装置后,泾渭分明地分裂成了两束,也就是测量它的 $\small z$ 方向自旋时,银原子的量子态坍缩到 $\small \left|z_+\right>,\left|z_-\right>$ 两个本征态上。
但 $\small \left|z_+\right>,\left|z_-\right>$ 其实是不可直接观察的,而我们“看见”的两束银原子,其实代表了两个具体的自旋磁矩的值。
比如处于 $\small \left|z_-\right>$ 的银原子,它之所以向下偏转,是因为它受到了一个向下的磁场力 $\small -F_z$,这个磁场力就来自于 $\small z$ 方向磁矩 $\small -\mu$ :
$\small -F_z=-\mu\frac{\partial B_z}{\partial z} \quad\scriptsize{(式6.9)}$
这样,观察到银原子向下偏转,其实就相当于测出了自旋磁矩的值 $\small -\mu$ ,而这正是 $\small \left|z_-\right>$ 对应的本征值。
- 第二个例子:定态薛定谔方程与原子能级
还记得我们第1课开头提到的、关于原子分立能级背后的“本质”的困惑吗?
我们当时不能理解,为什么原子核外电子会出在一些分立的能级上。
现在认识了算符、本征值和本征态的概念,我们就能给出一个看起来比较自然的(至少在数学上 )解释了:
经典力学中,能量也是一个力学量,因此,当我们关注一个粒子的能量的时候,就需要找出一个能量算符,它在量子力学中的正式名称叫作哈密顿算符(Hamiltonian),记作 $\small \hat{H}$
和其他力学量一样,能量的哈密顿算符也有对应的本征值和本征态,并且满足这样的关系:
$\small \hat{H}\left|a\right>=E_a\left|a\right> \quad\scriptsize{(式6.10)}$
其中 $\small \left|a\right>$ 就代表本征值 $\small E_a$ 对应的本征态。
而在坐标表象(以后我们会解释这个概念 )下,哈密顿算符可以表示为:
$\small \hat{H}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x) \quad\scriptsize{(式6.11)}$
(其中 $\small \hbar=\frac{h}{2\pi}$ 为约化普朗克常数, $\small m$ 为粒子质量,$\small V(x)$ 为势能 )
(以后我们会解释,为什么代表能量的算符会是这个样子 )
代入上式,我们就得到了:
$\small \left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\left|\psi\right> =E\left|\psi\right> \quad\scriptsize{(式6.12)}$
而态矢量 $\small \left|\psi\right>$ 在坐标表象下的具体形式,是我们熟悉的、或者至少听说的波函数 $\small \psi(x,t)$ (下节课我们将知道,一个函数如何被看作一个向量 )
于是我们可以将态矢量 $\small \left|\psi\right>$ 写成 $\small \psi(x,t) $,并且只考虑它与时间无关的部分(这可以通过分离变量实现,以后我们会解释 ),就得到:
$\small \left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi(x) =E\psi(x) \quad\scriptsize{(式6.13)}$
这就是定态薛定谔方程。
(注意:式6.13和式6.12的区别在于,式6.12中出现的是抽象的态矢量 $\small\left|\psi\right>$ ,而式6.13中出现的是具体的函数 $\small \psi(x)$ ,这意味着我们可以通过求解微分方程来得到态矢量的具体形式了 )
对于原子特有的球对称的电场而言,它可以写成球坐标形式,再代入势能项 $\small V(r)=-\frac{1}{4\pi\epsilon_0}\frac{e^2}{r}$ ,并新增电子-原子核体系的转动动能项 $\small \frac{\hat{\boldsymbol L}^2}{2\mu r^2}$,可得:
$\small \left[ -\frac{\hbar}{2\mu}\frac{1}{r^2}\frac{\partial}{\partial r} \left(r^2\frac{\partial }{\partial r}\right)+\frac{\hat{\boldsymbol L}^2}{2\mu r^2}-\frac{1}{4\pi\epsilon_0}\frac{e^2}{r} \right]\psi=E\psi \quad\scriptsize{(式6.14)}$
(左边那一长串合起来仍然是哈密顿算符 $\small \hat{H} $,虽然看起来复杂了点…… )
了解过偏微分方程的同学会知道,当给定了有限区域的或者周期性的边界条件时,这个方程会有一系列离散的特解 $\small \psi_n$ (第10课我们将会看到这一点)
而从向量的观点来看,这些特解 $\small \psi_n$ 其实就是哈密顿算符的本征态 $\small \left|E_n\right>$ ,而每个本征态对应的本征值 $\small E_n$ ,就是我们熟知的原子能级了。
从这个结果来看,线性微分方程和线性代数方程组其实是相通的,唯一可能让我们感到困惑的是:
微分方程是微分算子作用到函数上,而代数方程组是矩阵作用到向量上,这两者应该如何类比呢?
这个我们下节课再说,现在关于量子力学原理说得太多,信息量太大,我们该来一段总结了。
4) 总结与预告
其实,从第1课一路走到本课,我们已经可以模糊感觉到一个结论:
测量的概念是量子力学在物理上的核心与精髓——王正行《量子力学原理(第二版)》
所以,一旦理清楚测量问题的数学描述,量子力学的数学框架就能在我们脑中浮现出来了。
那我们就来总结一下这种数学描述方式吧:
一个经典力学量 $\small F$ 通常会对应一个算符 $\small \hat{F}$ ,它对应着一系列本征态 $\small {\left|F_a\right>}$ 和相应的本征值 $\small f_a$ ,并且满足本征值关系:
$\small \hat{F}\left|F_a\right>=f_a\left|F_a\right> \quad\scriptsize{(式6.4)}$
这可以简单理解成:当一个物理对象处于力学量力学量 $\small F$ 的本征态时,如果我们对它测量力学量 $\small F$ ,就会得到确定的结果、也就是本征值 $\small f_a$
而当物理对象处于这些本征态的叠加态时,如果再对它测量力学量 $\small F$ ,那么它的量子态就会随机坍缩到$ \small \hat{F}$ 的某个本征态 $\small \left|F_a\right>$ 上。
假设测量前的态矢量 $\small \left|\psi\right>$ 是 $\small \hat{F} $的本征态的线性组合:
$\small \left|\psi\right>=\sum_a{c_a\left|F_a\right>} \quad\scriptsize{(式6.6)}$
那么测量后,量子态坍缩某个到 $\small \left|F_a\right>$ 上的概率为 $\small |c_a|^2$
而坍缩发生后,我们会在经典世界里随机得到相应的测量结果、也就是本征值 $\small f_a$
并且,我们还能据此计算,对于处在量子态 $\small \left|\psi\right>=\sum_a{c_a\left|F_a\right>} $的物理对象测量 $\small F$ 时测量结果的期望值:
$\small \bar{f}=\sum_ac_a^*c_af_a \quad\scriptsize{(式6.8)}$
这将是我们将来定量计算不确定性关系、以及将经典动力学与量子态的演化规律联系起来的基础。
这里顺便说一句,对于所有经典可测量的力学量,它们的本征值都是实数(否则也就不可能被测量到了…… ),而它们对应的算符都属于一种叫做厄米算符(Hermitian Operator)的类型。
关于这一类算符的定义和运算性质,所有的量子力学课本都会介绍,但我们这里暂时先不展开,以后有需要的时候再补充。
最后,我们来提一个很多初学量子力学的同学都关心的问题:
量子态随机坍缩到本征态的这个过程是怎么发生的?
这个问题其实想起来挺有意思的,但为了防止走偏,我们这个系列不会就此展开讨论,而是采用简单粗暴的哥本哈根诠释,也是我们从第1课开始就一直在用的表述:
对物理对象测量某个力学量 $\small F$ 时,它的量子态会出于某种未知的原因、随机坍缩到 $\small F$ 的一个本征态上。
对其他解释(特别是多世界解释 )感兴趣的同学可以去读一读吴飙老师的《简明量子力学》第8章。
现在我们还是回到这个系列的主线。
在氢原子能级的例子中我们看到,对于一个线性微分方程而言,微分算子同样也有本征值和本征态(也就是微分方程的一组特解 )的概念。
但是问题来了,微分方程的未知函数是连续的,我们又该怎么理解它的向量性质呢?而微分算子看起来也不像矩阵的样子,我们又怎么理解它和矩阵之间的对应关系呢?
后面几节课,我们就要来尝试理解这个问题。
附录:关于态矢量“大小”
在前面讨论态矢量的“大小”和“方向”时,我们未加解释地给出了一个结论:
在量子力学中,一个态矢量没有“大小”的概念,对一个态矢量进行伸缩后,得到的仍然是同一个态矢量。
现在我们来解释为什么。
这背后的原因其实并不难理解,就和我们在第2课中提到的归一化条件有关。
我们知道,任何态矢量都可以表示成某个力学量的本征态的线性叠加:
$\small \left|\psi\right>=\sum_ac_a\left|F_a\right> \quad\scriptsize{(式6.6)}$
叠加系数 $\small c_a$ 的模平方 $\small \left|c_a\right|^2=c_a^*c_a$ 就对应着测量力学量 $\small F$ 时、态矢量坍缩到本征态 $\small \left|F_a\right>$ 的概率。
而我们知道,所有可能结果的概率加起来一定等于1,即:
$\small \sum_a\left|c_a\right|^2=1 \quad\scriptsize{(式6.7)}$
这就是态矢量的归一化条件,而这也等价于所有态矢量与它自身的内积为1,也就是态矢量的“大小”为1.
这样,态矢量就不再需要“大小”的概念,因为归一化条件强行钦定了它们的模长,都是1.
于是,对于任意两个态矢量,只要它们的“方向”一致,我们就认为它们是同一个。
编辑于 2022-08-11 19:15








