物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第3课。
了解本系列其他文章,请收藏目录:
0) 开篇语
在前两课中,我们以著名的“薛定谔的猫”思想实验作为引子,引入了一个名叫态矢量的新物理量,并用线性代数中的向量来解释了它的诸多“物理特性”,以此打开了量子力学的大门。
而带着对叠加态及其向量性质的理解,我们就可以一个个弄明白我们在开篇提到过的那些困惑。
比如本课中将要讨论的不确定性原理 (Uncertainty Principle)
(注意:本课只是一次定性体验,虽然会有一些简单计算,但还没有对不确定性关系进行严格推导 )
它可以这样表述:
我们不能通过测量同时确定两个不对易(以后解释什么是不对易 )的物理量,比如位置和动量,因为对其中一个的测量行为会干扰被测对象的状态,导致另一个物理量无法确定。
看完这句话后,问题就来了:“测量行为会干扰被测对象的状态”这句话应该怎么理解呢?
可能各位心里对此都有自己的猜测,但作者敢肯定的是,对于没有学过量子力学的同学而言,这个猜测有 $\small \lim_{n\rightarrow\infty}{\sum_{k=1}^{n}{\frac{9}{10^k}}}$ 的可能是错的。
那正确的理解是什么样的?让我们从另一个虚构的量子事件开始探寻……
1) 一颗奇怪的Q糖
(原创声明:本故事系作者原创,如需转载,请征求作者同意并注明出处 )
在一个月高风黑、伸手不见黑夜的五指,我们收到了一个神秘人寄来的小盒子。
随盒子寄到的还有一张说明书:
盒子里有一颗不普通的糖,名叫Q糖。注意,是Q糖,不是QQ糖。
它的味道有时是甜的,有时是酸的;它的颜色有时是红的,有时是蓝的。
当你品尝它时,请不要一口吃完,建议你放进嘴里尝一口味道,再拿出来再看一眼颜色。
多尝试几次,你会发现一些神奇的规律,也会理解这颗Q糖名字里‘Q’的含义。
好了,请用你的眼睛和舌尖开始探索它的规律吧,祝你用餐愉快。
看完说明书,我们决定先看看糖的颜色。
于是我们打开了盒子,看到一颗小硬糖,颜色是蓝色的。

接下来,我们把糖放进嘴里,尝了尝它的味道:是酸的。

这时,我们想起了说明书上的建议,于是就把糖从嘴里拿出来,重新看了一眼它的颜色……然后灵异事件果然发生了:糖变成了红色。

百思不得其解的我们,带着一丝好奇和一丝疑惑,再次把糖放进嘴里,结果灵异事件再次发生:糖变甜了。

通过前面这两次尝试,我们似乎找到了一条规律:
每尝一次味道后,糖的颜色就会变;而每看一次颜色后,糖的味道就会变。
为了验证这个规律是否成立,我们又多做了几次重复实验,结果……事情好像并不是我们想的那样。
多次尝试的结果是什么呢?
我们发现,有时候尝完味道再去看颜色时,入口前蓝色的糖还是蓝色、红色的糖也还是红色,但有时候两种颜色又会相互转变,并且变或不变与我们尝到的味道无关;
糖的味道也有着同样的情况:并不是每次看完颜色之后、再把糖放到嘴里,味道就一定会变,变或不变看起来也是完全随机的。
所以,多做几次尝试后,我们反而看不出什么规律来了。
但事情并没有让人绝望,有一点值得欣慰的是,经过细心观察和统计,我们发现了两个规律:
第一,每次尝完糖的味道之后重新观察它的颜色,变色和不变色的情况各占一半;同样,每次看完糖的颜色之后重新品尝它的味道,变味和不变味的情况也各占一半。

第二,如果我们尝完糖的味道之后,不去看糖的颜色,那么即使我们把糖拿出来再放进嘴里尝味道,它的味道也不会变,无论重复多少次都不会变;颜色也一样,只要我们不去尝味道,那么我们无论多少次重复观察糖的颜色,它都还是原来的样子。
这背后是什么神秘力量在作祟呢?
这时候,我们想起了这颗糖的名字:Q糖。也许,这里的Q的意思就是Quantum?
既然想到了这一点,那就试试用量子力学来解释吧。
我们可以尝试用第1课中提到的叠加态,来理解这颗看起来变幻莫测的Q糖,并且用叠加态的数学形式来理解上面发现的统计规律。
2) Q糖的叠加态
我们在第1课中回顾薛定谔猫的思想实验时知道:
当我们没有打开盒子去观察猫的状态时,它处于生和死的叠加态,而一旦我们去观察,它就会随机坍缩到生或死中的一个确定状态,此后再去观察时,它的状态就不再会改变。
类比糖的例子:
当我们观察了Q糖的颜色之后,颜色也会变成红或蓝中的一个确定状态,以后只要不做其他干扰,那么再无论观察多少次,颜色都不会再改变;
或者我们品尝了Q糖的味道之后,味道也会变成甜或酸中的一个确定状态,以后只要不做其他干扰,无论再品尝多少次,味道都不会再改变。
这看起来没有什么奇特的,奇特出现在我们交替进行两种行为的时候:
当我们确定了糖的颜色之后,再去品尝糖的味道,味道又会随机坍缩到酸或甜两种状态,且概率各半;反过来,确定味道之后再去观察颜色,也有同样的情况。
这也就意味着:
糖的颜色处于确定状态时,味道就处于不确定的叠加态;而味道处于确定状态时,颜色就会处于不确定的叠加态。
现在我们就用第1课提到的那些数学原理来分析这件事情。
在第1课中我们知道,对于某个需要观测的量而言,可以被观测到的状态,在量子力学中称为本征态。
对应到本例中:
糖的味道的本征态就是甜和酸,用 $\small \left|a_1\right>,\left|a_2\right> $来表示;
而糖的颜色的本征态就是蓝色和红色,用 $\small \left|b_1\right>,\left|b_2\right>$ 来表示。
于是我们可以用本征态的语言,进一步描述前面的叠加态关系:
- 当味道处于确定的状态、也就是味道的本征态 $\small \left|a_1\right>,\left|a_2\right>$ 的其中一个时,颜色处于叠加态,变得不确定,此时去重新观察颜色,会分别以1/2的概率得到“红”($\small \left|b_1\right>$)和“蓝”( $\small \left|b_2\right>$ )的状态;
- 当颜色处于确定的状态、也就是颜色的本征态 $\small \left|b_1\right>,\left|b_2\right>$ 的其中一个时,味道处于叠加态,变得不确定,此时去重新品尝味道,会分别以1/2的概率得到“甜”($\small \left|a_1\right>$)和“酸”($\small \left|a_2\right>$)的状态。
怎么理解这种“互为叠加态”的关系呢?
本着用线性代数理解量子力学的宗旨,当事情变得过分诡异无法理解时,我们就回到线性代数,从数学中寻找答案。
3) 线性代数复习课:基底变换
我们先来看一个二维平面上的案例:
假设二维平面上有两组正交基底,分别记为 $\small { \boldsymbol a_1,\boldsymbol a_2} $和 $\small { \boldsymbol b_1,\boldsymbol b_2}$ ,它们在同一平面上成45度夹角,如下图:
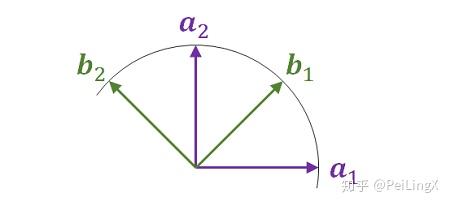
那么我们可以用其中一组基底 $\small { \boldsymbol b_1,\boldsymbol b_2} $的线性组合来表示另外一组基底 $\small { \boldsymbol a_1,\boldsymbol a_2} $:
$\small \begin{cases}\boldsymbol a_1=\frac{1}{\sqrt{2}}(\boldsymbol b_1-\boldsymbol b_2) \\ \boldsymbol a_2= \frac{1}{\sqrt{2}}(\boldsymbol b_1+\boldsymbol b_2) \end{cases} \quad\scriptsize{(式3.1)}$
写成矩阵形式就是:
$\small \begin{bmatrix}\boldsymbol a_1\\ \boldsymbol a_2 \end{bmatrix} =\frac{1}{\sqrt{2}} \begin{bmatrix} 1&-1\\1&1 \end{bmatrix} \begin{bmatrix} \boldsymbol b_1\\ \boldsymbol b_2 \end{bmatrix} \quad\scriptsize{(式3.2)}$
同学们,看到这个,有没有在冥冥中感受到来自智慧女神的启发?

来,我们再回头看这颗Q糖。
4) 神奇Q糖的数学解释
现在我们将前面的数学关系类比到Q糖的状态上来。
我们先以味道的状态为例:当我们去品尝Q糖的“甜度”时,它的量子状态就随机落到了“甜”或“不甜”两个本征态的其中一个上面。
在平面上表示,“甜”和“不甜”就分别对应着 $\small \left| a_1\right>,\left| a_2\right>$ 两个向量。
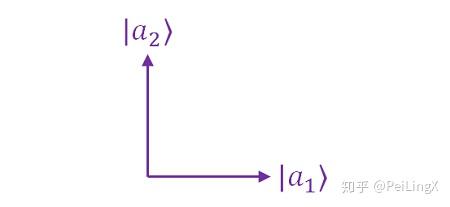
如果我们品尝了Q糖的味道、发现它是甜的,那么它的状态就落到了味道的本征态 $\small \left|a_1\right>$ 上。
而根据前面的描述,当它的味道处于确定状态时,它的颜色就变得不确定了。
用量子语言来说,就是Q糖的颜色变成了“红”和“蓝”两个本征态的叠加。
为了从数学上描述这一点,我们再搞一对基底,记为 $\small \left| b_1\right>,\left| b_2\right>$ 。它们就对应颜色的“红”和“蓝”两个本征态。
现在,我们就可以从直观的“几何”图景来解释前面的诡异现象了。
我们不妨将前面提到的二维平面上的两组基底 $\small { \boldsymbol a_1,\boldsymbol a_2} $和 $\small { \boldsymbol b_1,\boldsymbol b_2}$ 之间的几何关系,换成抽象的态空间中两组基底 $\small \left| a_1\right>,\left| a_2\right>$ 和 $\small \left| b_1\right>,\left| b_2\right> $的“几何”关系:
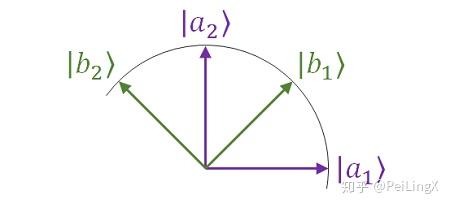
然后我们来看看会得到什么。
根据前面对两组向量基底几何关系的分析,我们知道:
$\small \left| a_1\right>=\frac{1}{\sqrt{2}}(\left|b_1\right>-\left|b_2\right>) \quad\scriptsize{(式3.3)}$
这就意味着,糖的味道确定(处于本征态 $\small \left|a_1\right> )$时,颜色就处在了叠加态中,所以,如果接下来我们再去测量它的颜色,就会随机得到“红”或“蓝”的结果。
而这两个结果的概率,就是叠加系数的模方,于是可以算出两个结果分别对应的概率:
$\small \begin{cases} P(\left| b_1\right>)&=\left(\frac{1}{\sqrt{2}}\right)^2&=\frac{1}{2}\\ P(\left| b_2\right>)&=\left(-\frac{1}{\sqrt{2}}\right)^2&=\frac{1}{2} \end{cases} \quad\scriptsize{(式3.4)}$
也就是说,此时我们以各1/2的概率得到“红”或“蓝”的结果。
根据同样的思路,我们也可以解释为什么观察完颜色后再去品尝味道,也会以各1/2的概率得到“酸”或“甜”的结果。
到此,一切真相大白。
接下来,我们就可以整理一下思路,来回答本文开头提到的问题了:
如何理解“测量行为会干扰被测对象的状态”?
5) 确定性的丧失
在第1课的开头,我们提到过这样两句话:
经典物理描述一个物理对象的状态,是用具体的力学量,比如位置、速度、动量、能量等……
而量子力学描述一个物理对象状态的方式,说起来非常简洁,只需要一个量:叫做态矢量。一个态矢量即包含了物理对象的一切经典力学量的(概率 )信息。
从这个虚构的量子事件中,我们其实可以看到一些端倪:
如果是一颗“经典”的糖,我们需要用“味道”和“颜色”两个物理量来描述它的状态;
但对这颗量子糖而言,它的状态用态空间的一个向量(即态矢量)来描述即可。
这样的物理系统的确简洁了许多,但同时也暗藏了一个重大的秘密:就是确定性的丧失,因为量子糖不再可能同时拥有确定的味道和颜色。
比如,当它的味道确定时,态矢量就落到了味道的本征态 $\small \left|a_1\right>$ 或 $\small \left|a_2\right>$ 上,而这两个态矢量都是颜色的本征态 $\small \left| b_1\right>,\left| b_2\right>$ 的线性叠加,这也就意味着颜色不再确定。
从这个角度来看,不确定的来源,的确可以理解为测量行为对被测对象的状态产生了干扰,但这是量子意义上的干扰,和经典意义的理解有着本质区别。
比如我们理解动量和位置的不确定性关系时,一种错误的理解方式是:
测量一个粒子的位置时,测量中某个动作(比如发射一粒光子 )改变了粒子的动量,因此粒子的动量无法同时测准。
在这种理解中,粒子的动量虽然被改变了,但它仍然是一个确定值,只是因为测量手段的限制,变得“测不准”而已,这显然不是“量子式的”理解方式。
而正确的、“量子式的”理解方式是:
一旦粒子的位置确定,它的动量就处于叠加态,没有确定的值,直到我们去测量它的动量时,才随机给出一个动量值来。
类比到本文提到的Q糖的例子,错误的理解方式就是:
品尝味道这个动作,干扰了糖的颜色,使他变成蓝色或红色,但这个颜色在完成品尝的那一刻就确定了。
而正确的、“量子式的”理解方式是:
品尝味道这个动作,使糖的状态变成了味道的某个本征态,同时也是颜色的两种本征态的线性叠加,这就意味着,在下一次观察颜色之前,糖的颜色是不确定的。
这才是不确定性原理的正确打开方式。
不过需要说明的是,我们这个虚构的量子事件中,态空间是二维的;而在真实的物理世界中,态空间是无穷维的,而相应的态矢量也是一个无穷维向量,这个无穷维向量就是波函数。
至于如何将一个函数和一个向量对应起来,我们以后会慢慢体会。
将来明白了这个对应关系之后,量子力学的数学框架就会在我们眼中就会变得非常清晰;而且描述不确定性原理的那个神秘式子 $\small \Delta x\Delta p\sim \frac{\hbar}{2}$ 的来源也会被交待得明明白白。
6) 结语和预告
本文中,我们用一个虚构的场景:量子糖的“味道”和“颜色”之间的不确定性关系,从数学的角度粗略体验了不确定性原理的理解方式。
但到此为止,我们都还只是在虚构的物理情形中幻想,还没有体验过真正的量子力学带来的快感。
在下一课中,我们就会通过介绍一个历史上真实存在过的、可以看成“Q糖实验”的现实版本的实验:斯特恩-盖拉赫(Stern-Gerlach)实验,来真正迈进量子力学的大门。
编辑于 2021-11-30 13:21




