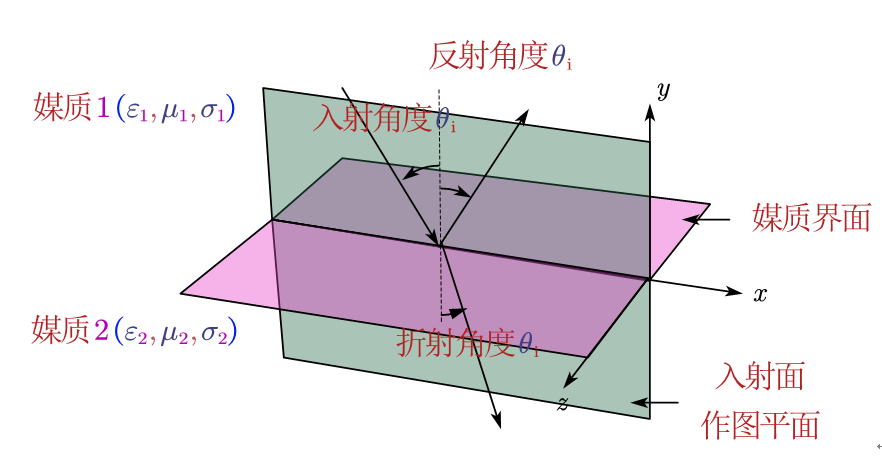
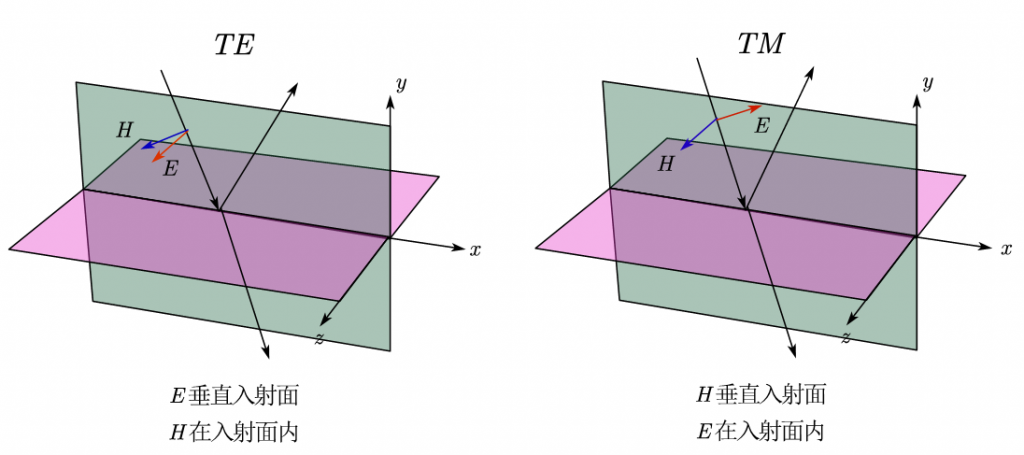
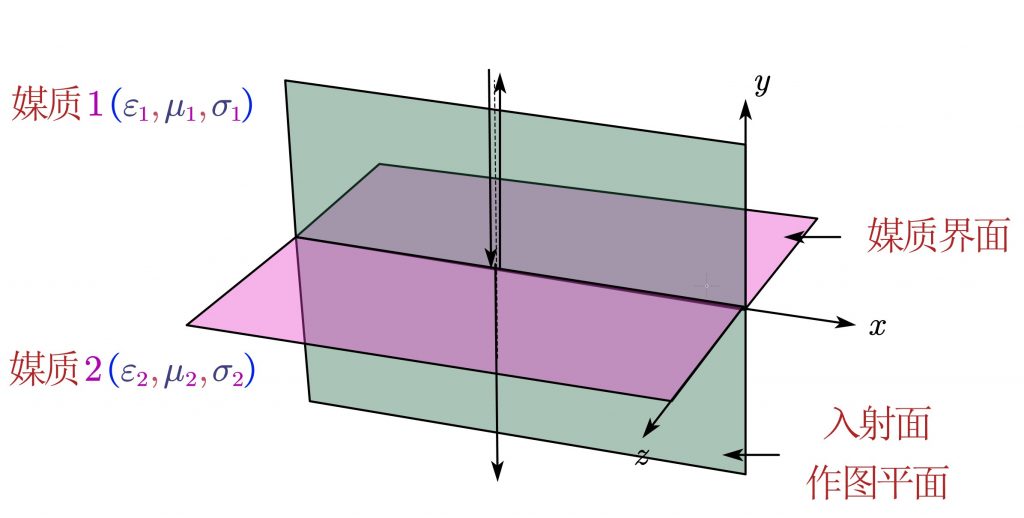
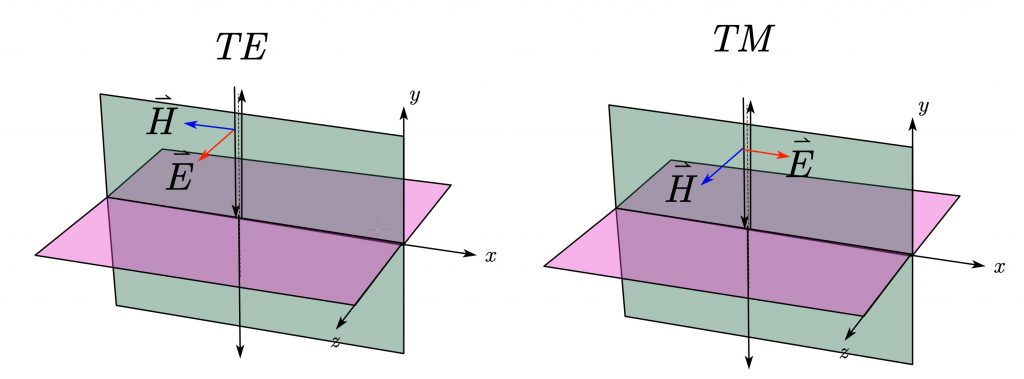
亥姆霍兹方程描述了无损耗媒质中时谐电磁场的场量约束关系。均匀平面波是其在最简情况下的一种解。
当均匀平面波向正z轴传播时,电场强度将垂直于传播方向,可以电场强度方向为x轴。
仿真计算作图时,媒质参数为:\({\varepsilon _r} = 2,{\mu _r} = 1,\sigma = 0\)
一、电场强度
电场强度矢量的(相量)表达式为:
\[\vec E = {\hat a_x}{E_0}{e^{ - jkz}}\]
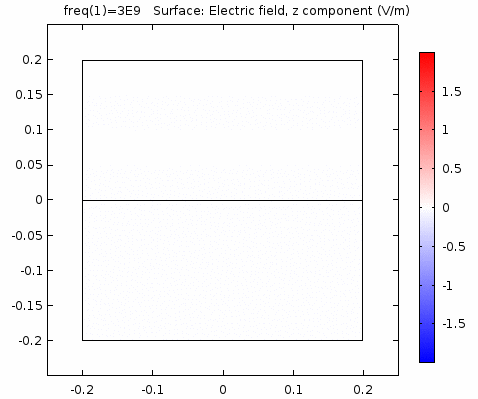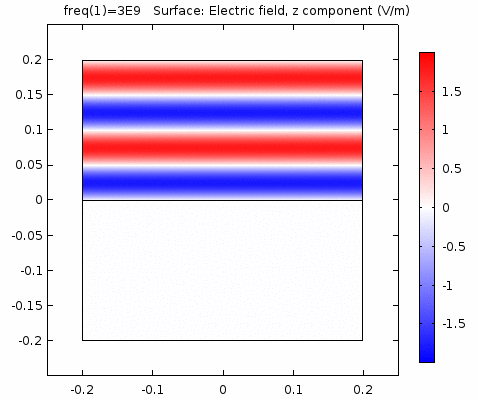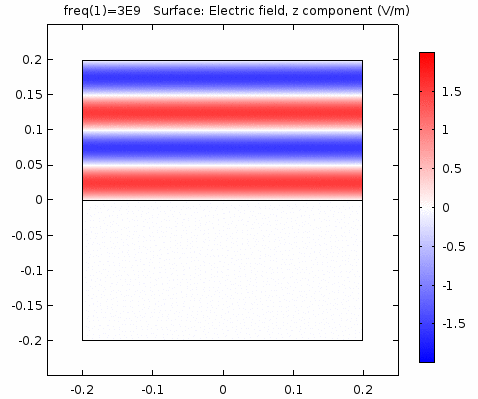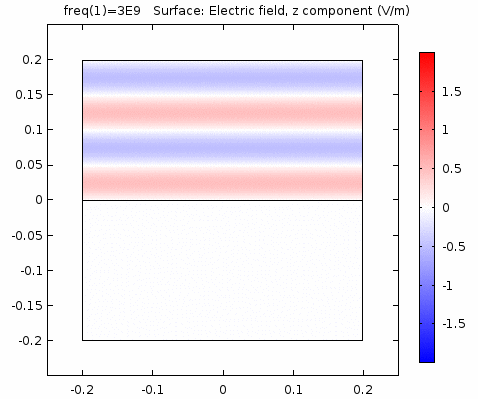
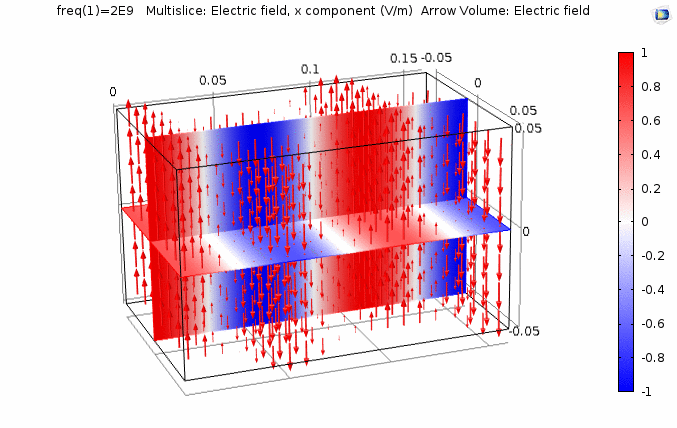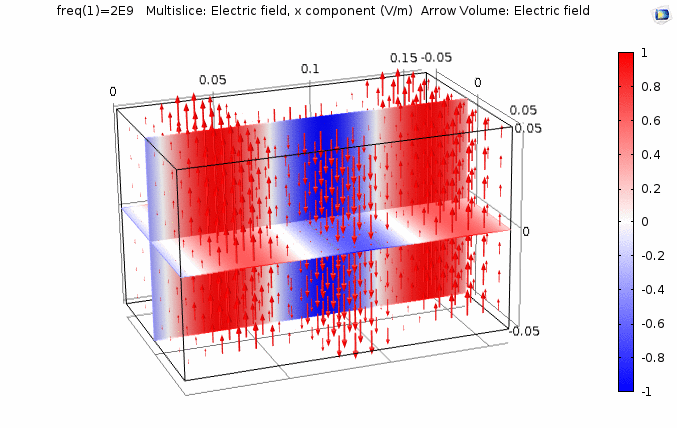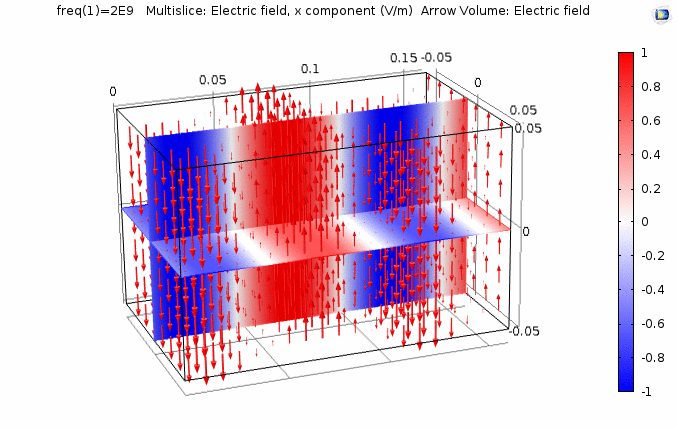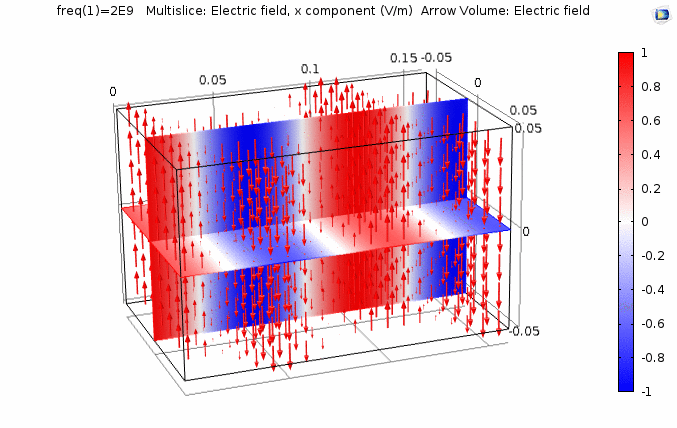
下图画出了振幅\(E_0=1\),相位常数\(k=41.97rad/s\)时,方形区域内的电场强度矢量箭头。同时用着色方式画出了\(x=0\)平面、\(y=0\)平面上的电场强度大小。
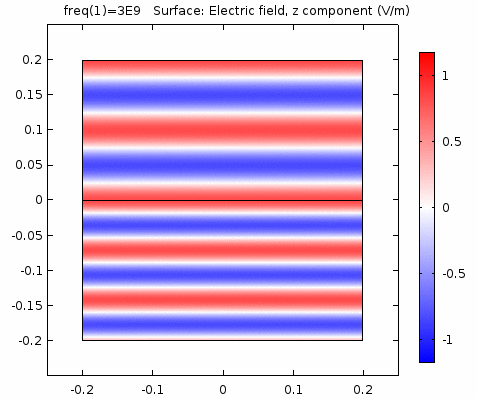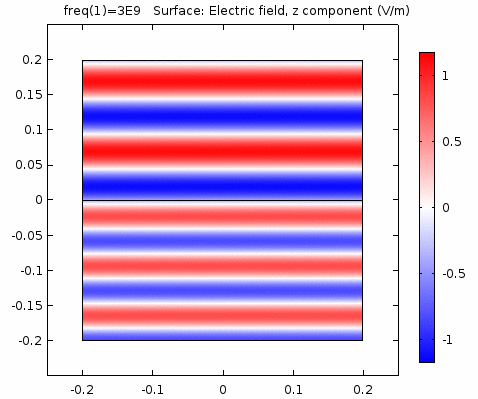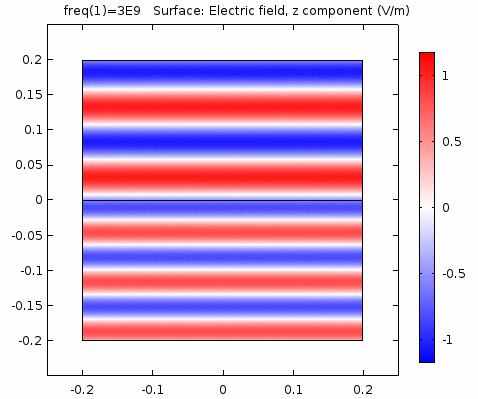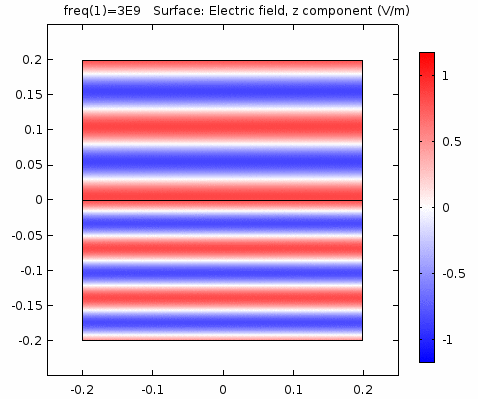
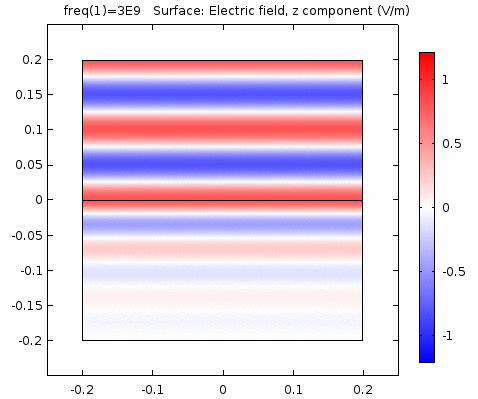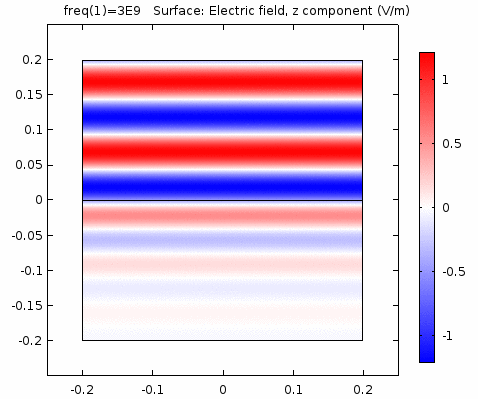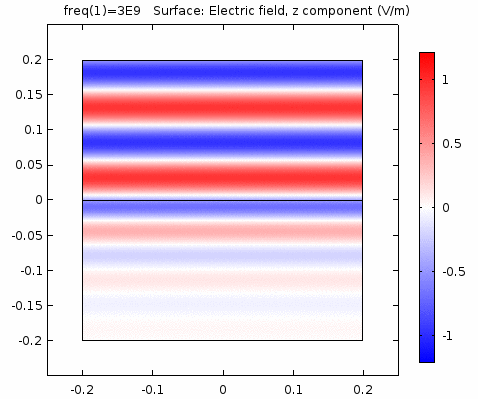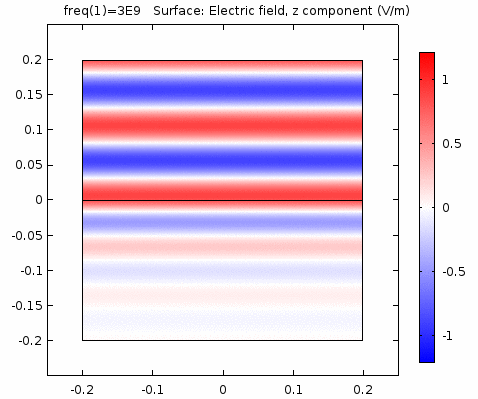
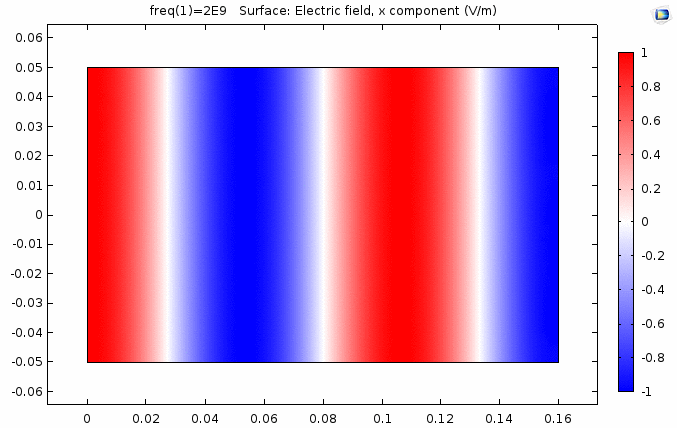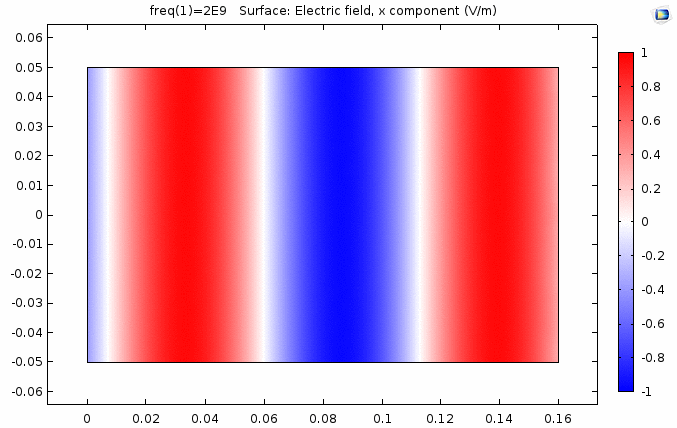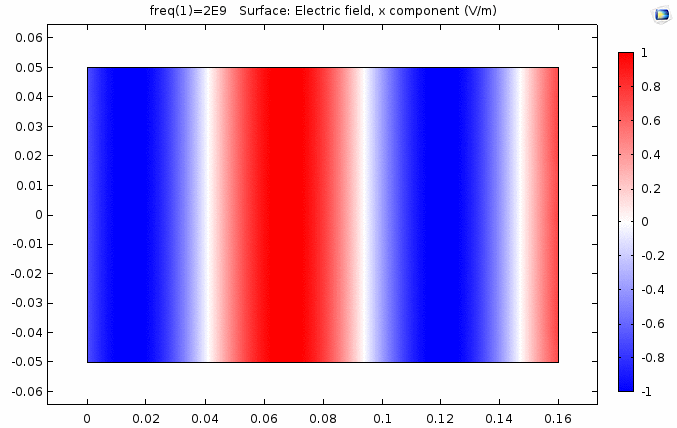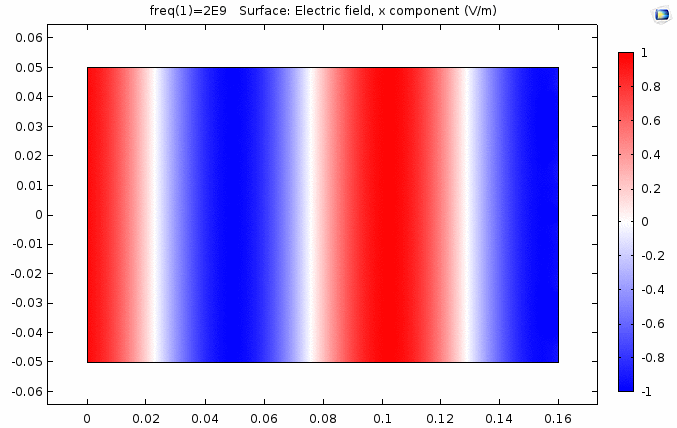
用二维图表达时,一般仅用着色方式显示分量大小。如\(x-z\)平面上的电场强度\(E_x\)分量如下图。
二、磁场强度
磁场强度既与传播方向垂直,又与电场强度方向垂直,沿y轴方向。
磁场强度表达式为:
\[ \vec H ={\hat a_y}{H_0}{e^{ - jkz}} = {\hat a_y}\frac{{{E_0}}}{\eta }{e^{ - jkz} }\]
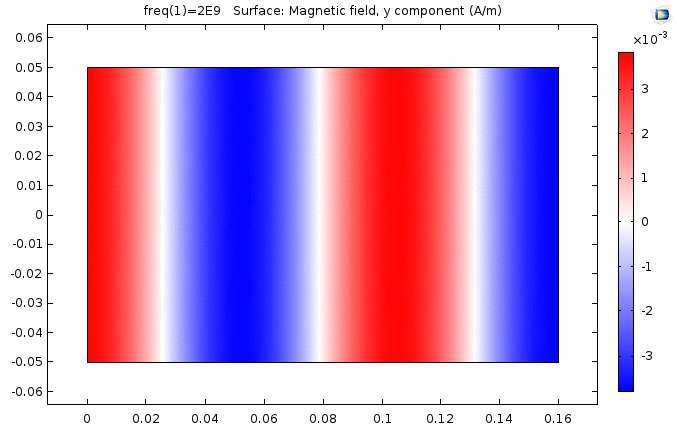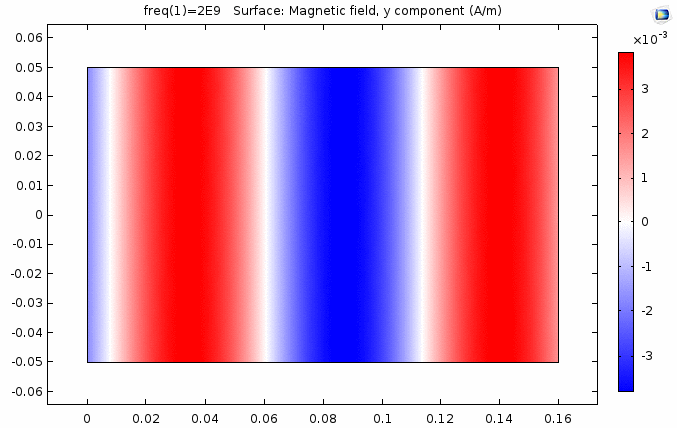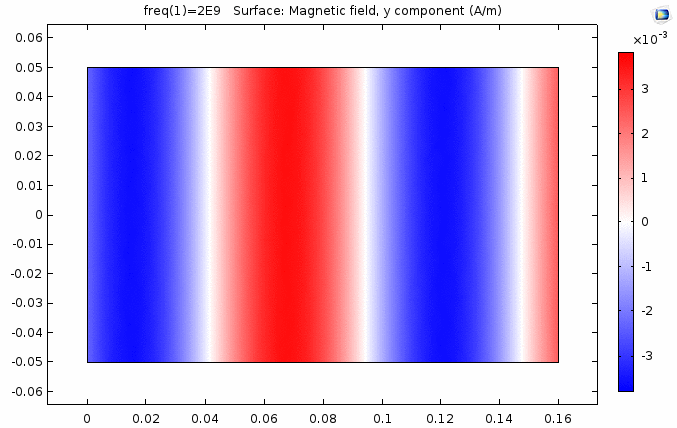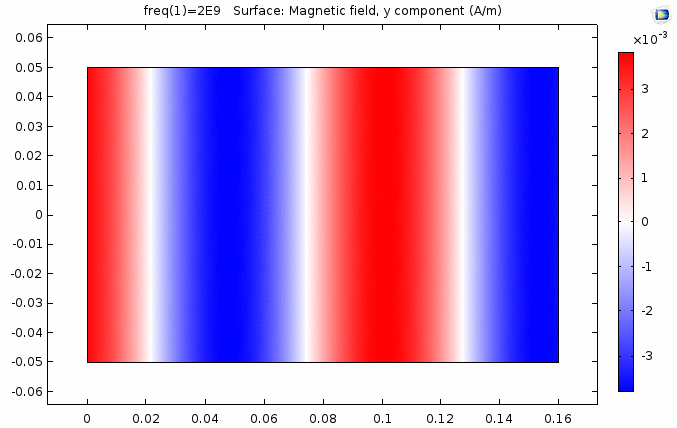
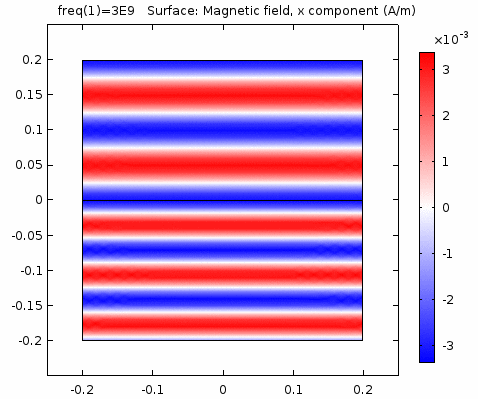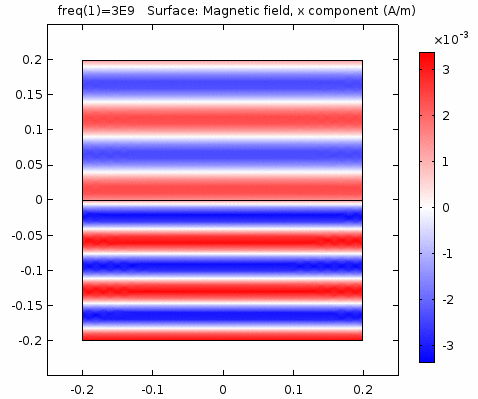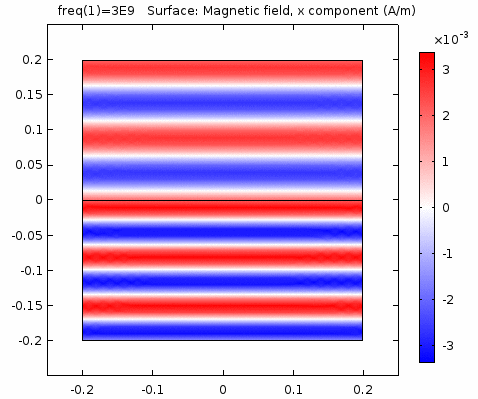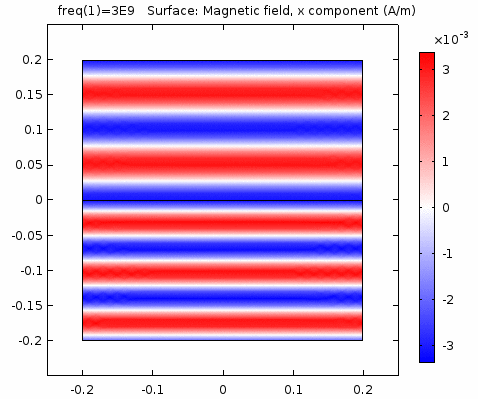
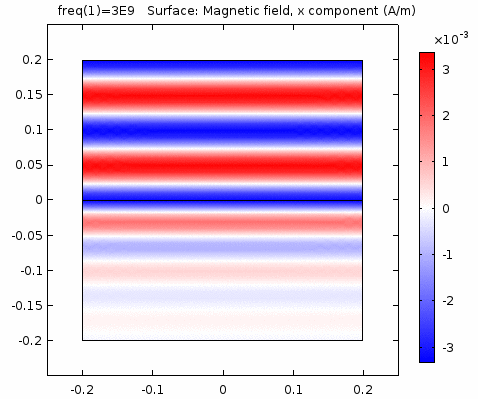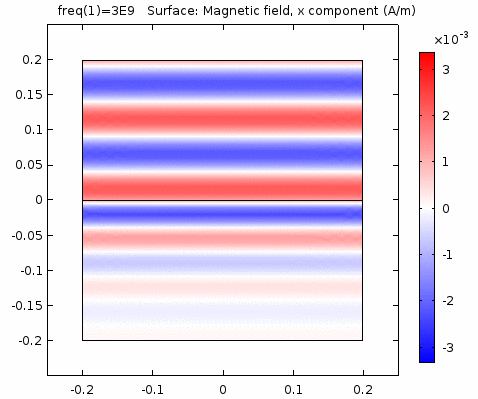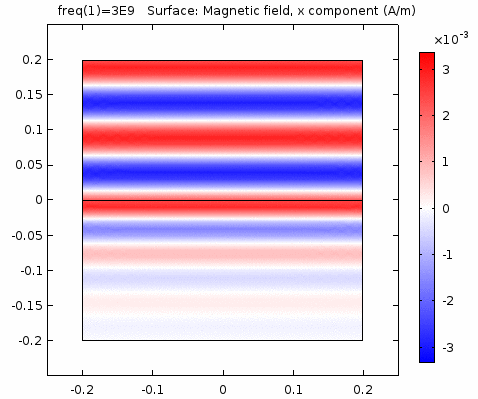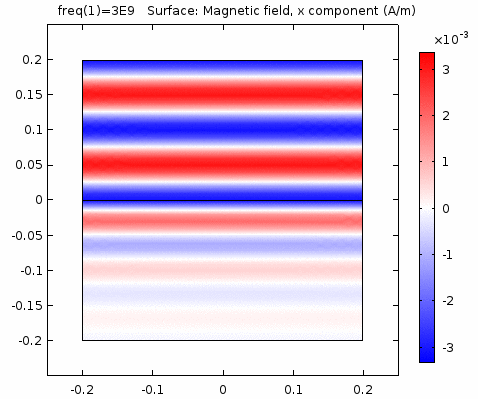
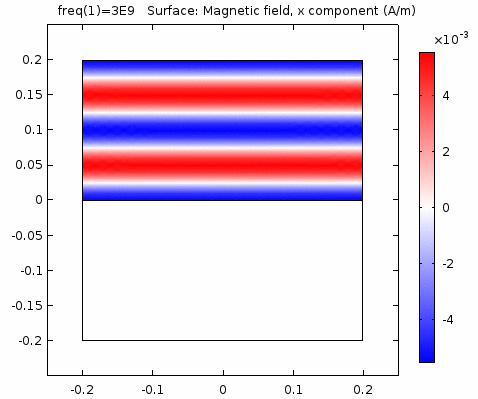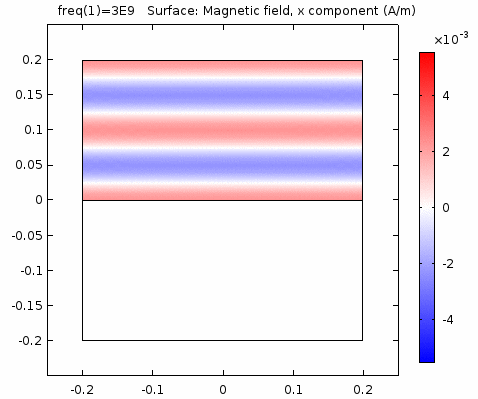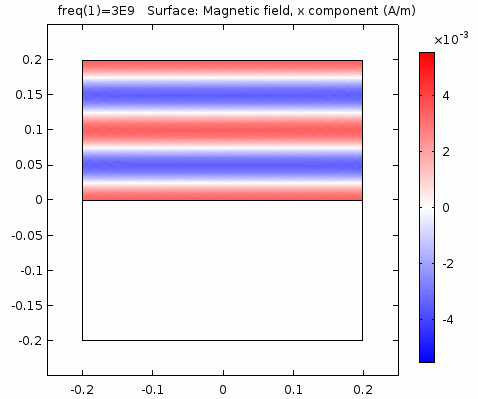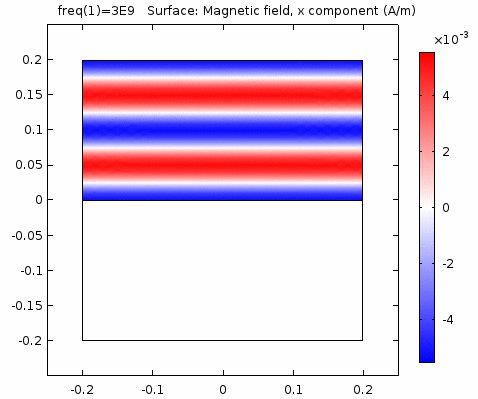
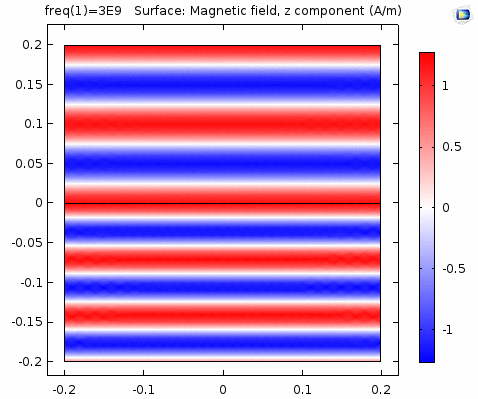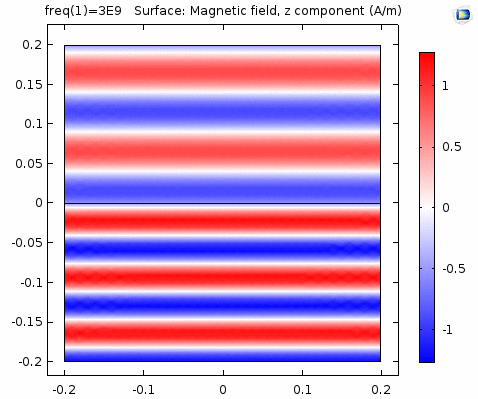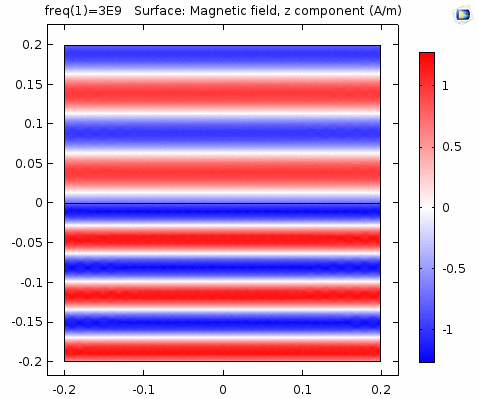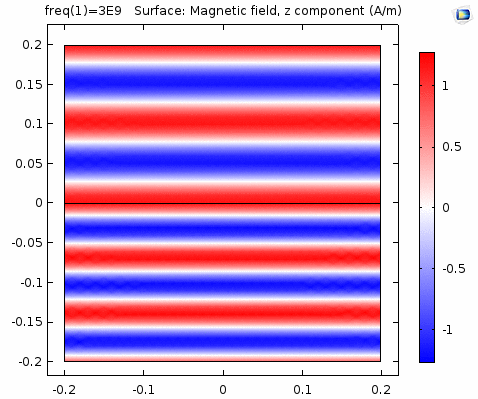
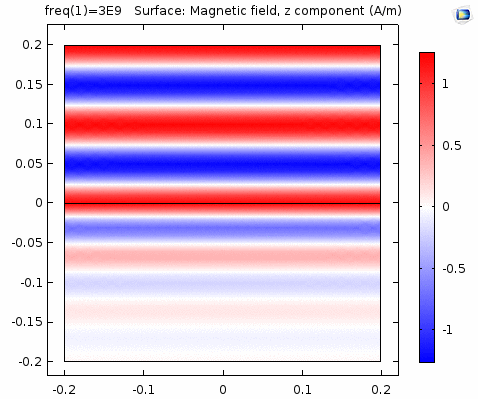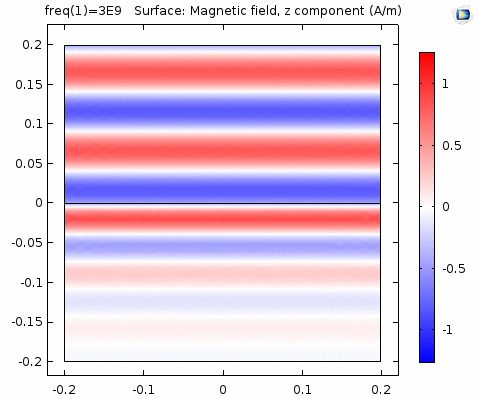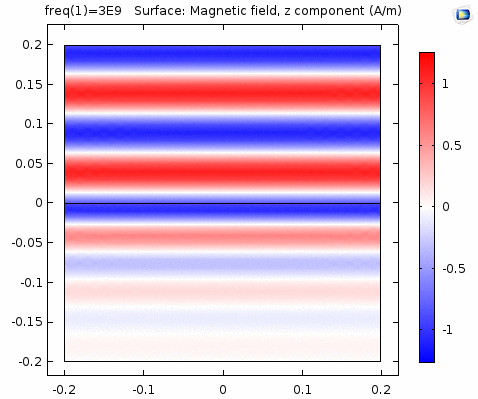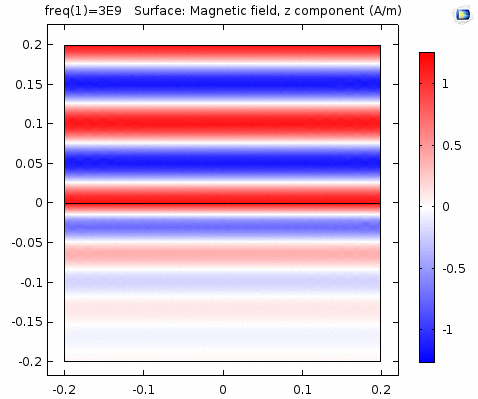
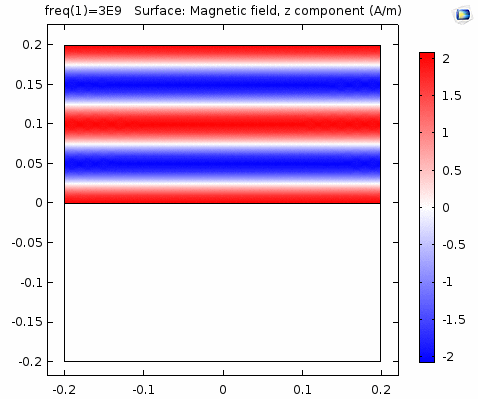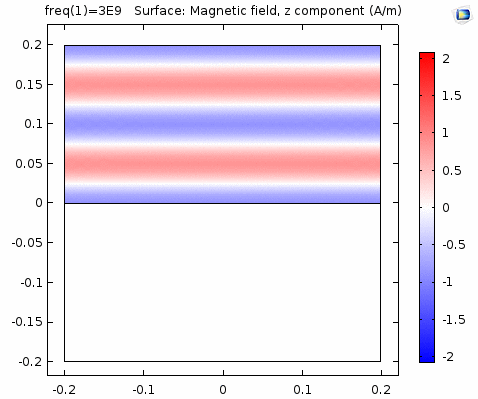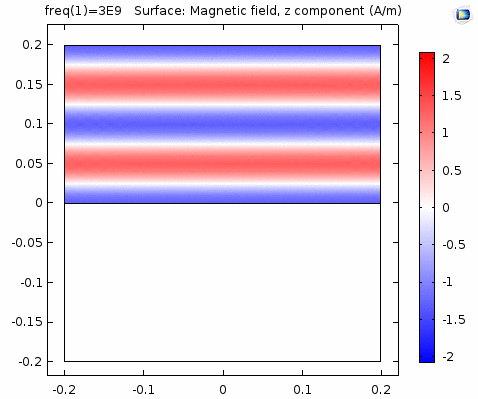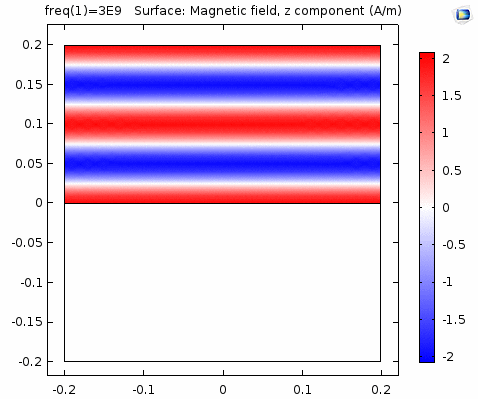
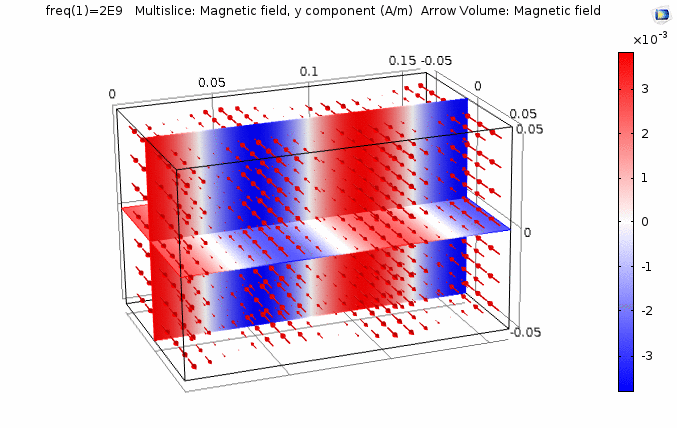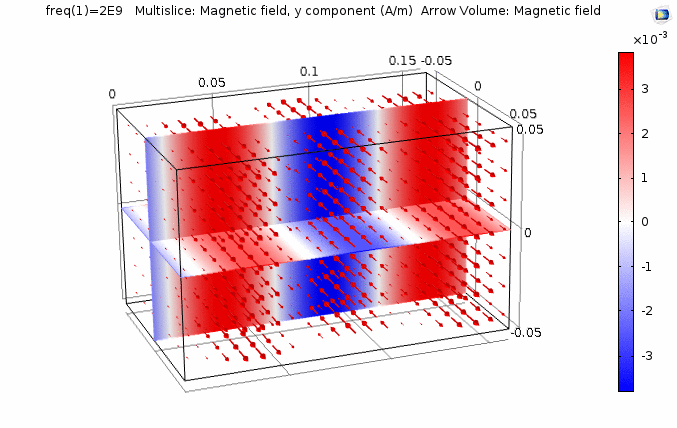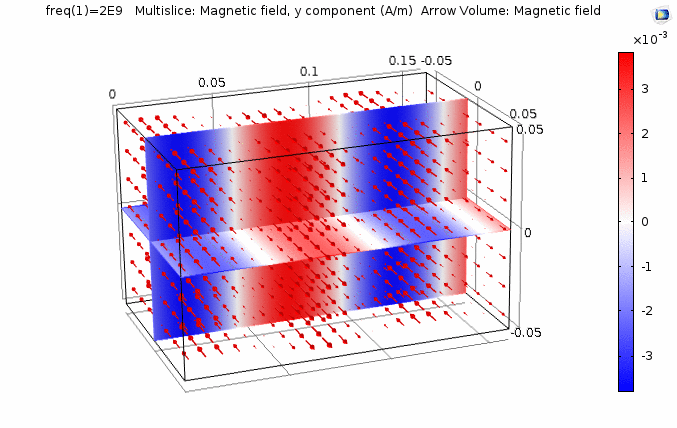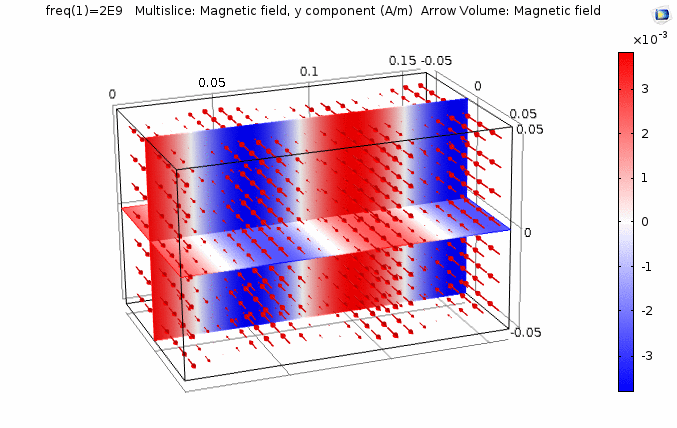
下图画出了电场振幅\(E_0=1\),波阻抗\(\eta =261.8 \Omega\),相位常数\(k=41.97rad/s\)时,方形区域内的磁场强度矢量箭头。同时用着色方式画出了\(x=0\)平面、\(y=0\)平面上的磁场强度\(H_y\)大小。
用二维图表达时,一般仅用着色方式显示分量大小。如\(x-z\)平面上的电场强度\(H_y\)分量如下图。